Autor: Ana Martinčević
Projekt: “Teselacija i Pitagorina poučak”
Cilj projekta:
Upoznati učenike s Pitagorinom poučkom i primjenom geometrijskih oblika u mozaicima, te im omogućiti da kroz praktične aktivnosti i zadatke razviju vještine razmišljanja, rješavanja problema i kreativnog izraza.
Umna mapa Pitagorin poučak
- Učenici će izraditi umnu mapu o Pitagorinom poučku u digitalnom alatu po želji
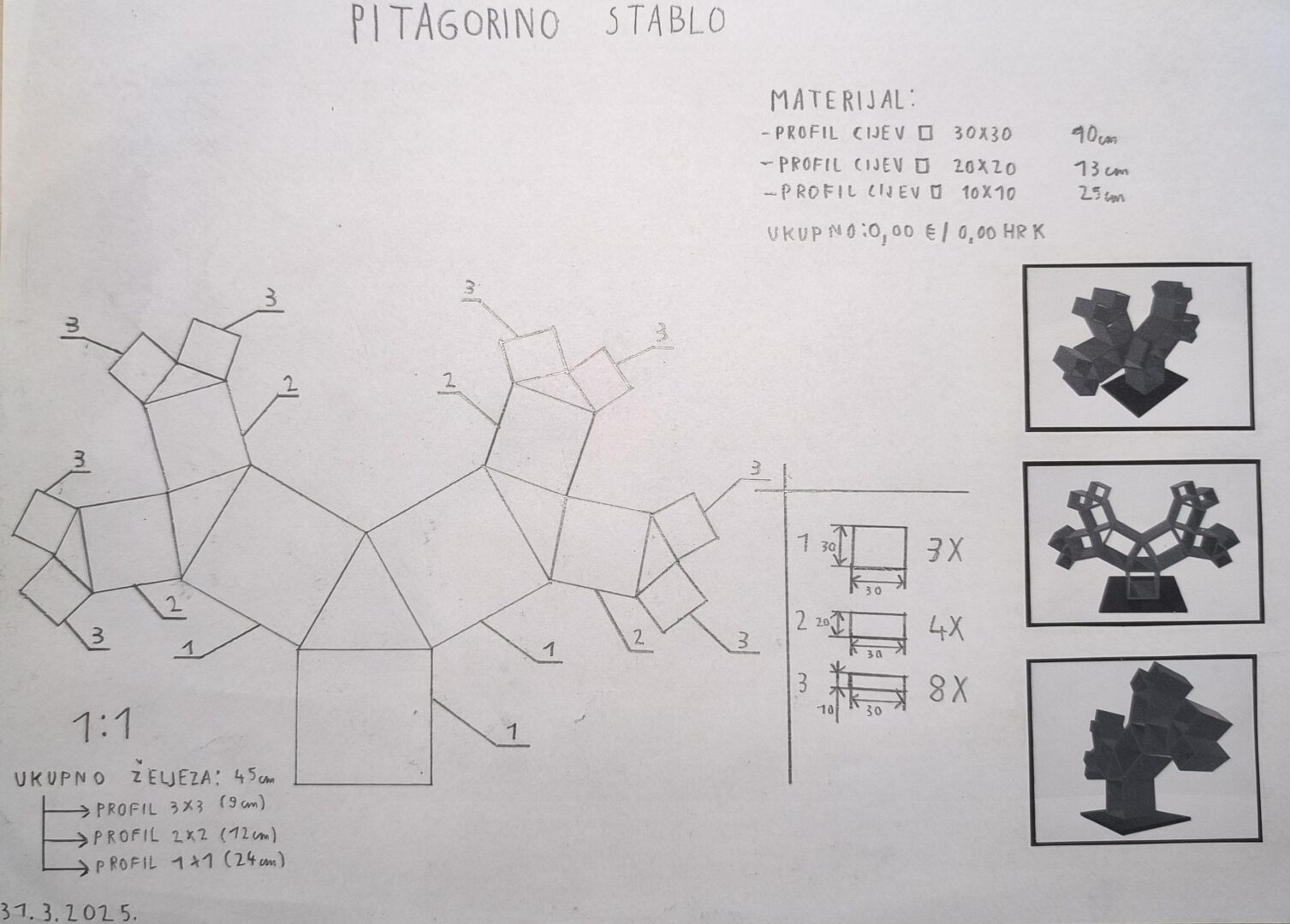
Pitagorino stablo
Pitagorino stablo je zanimljiv geometrijski koncept koji pomaže učenicima da bolje razumiju Pitagorin poučak kroz vizualizaciju i kreativnost.
Pitagorino stablo je matematička figura napravljena od pravokutnih trokuta i kvadrata. Počinje s pravokutnim trokutom, gdje su kvadrati nacrtani na svakoj od njegovih stranica. Zatim se postupak ponavlja – na katetama se ponovno crtaju pravokutni trokuti i kvadrati, stvarajući strukturu nalik stablu.
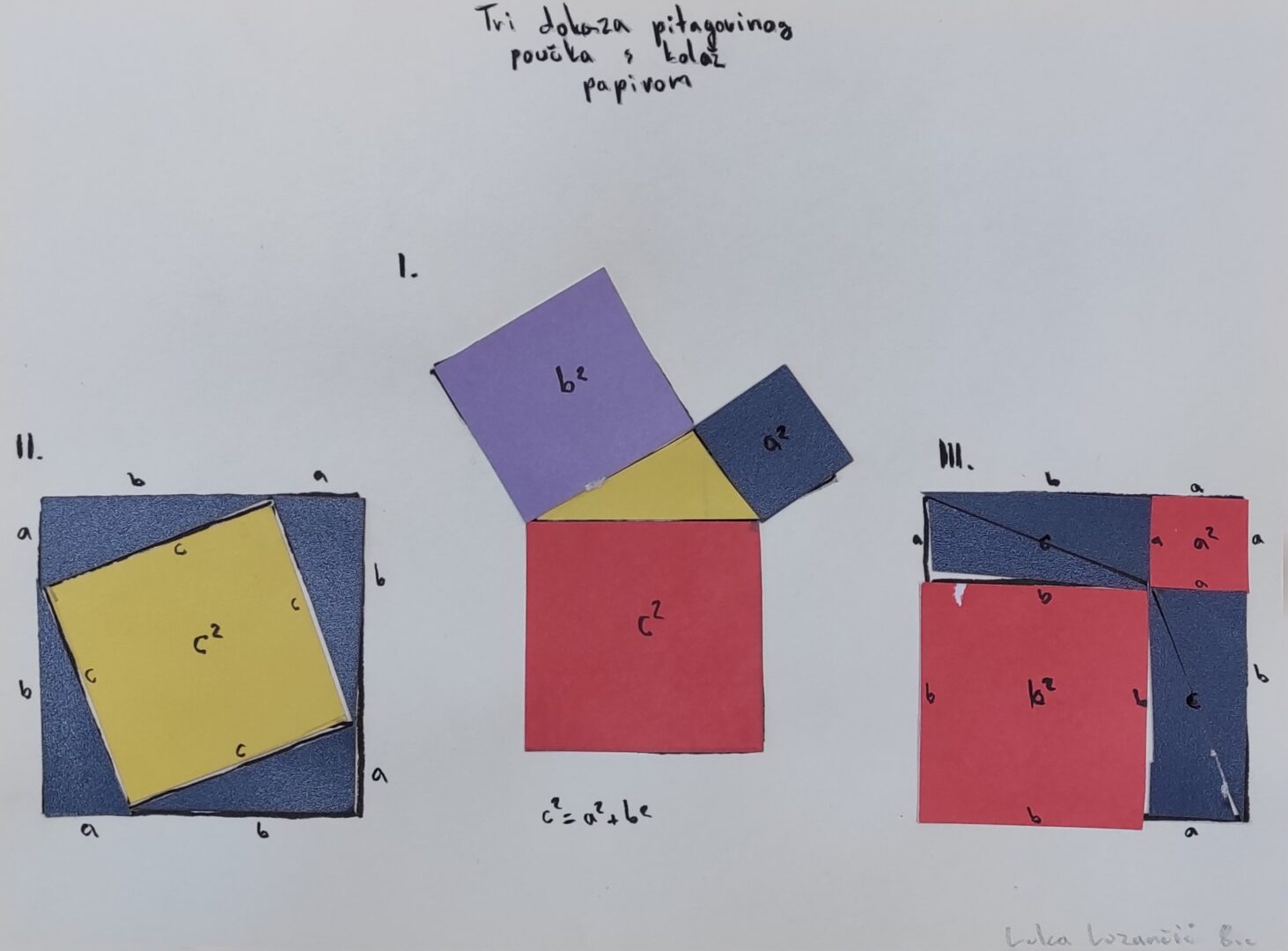
Dokazi Pitagorina poučka
Pitagorin poučak, jedan od najpoznatijih matematičkih teorema, ima brojne dokaze koji se temelje na različitim matematičkim pristupima. Evo tri najpoznatija dokaza, zajedno s objašnjenjem ideja koje stoje iza njih i ishoda:
1. Dokaz pomoću geometrijskih kvadrata
Ideja dokaza:
Ovaj dokaz koristi vizualni pristup pomoću kvadrata nad stranicama pravokutnog trokuta. Na svakoj strani trokuta nacrta se kvadrat. Površina kvadrata na hipotenuzi jednaka je zbroju površina kvadrata na katetama.
Postupak:
1. Prvo se pokazuje da su dijelovi kvadrata na hipotenuzi jednaki površinama kvadrata na katetama.
2. Premještanjem dijelova unutar kvadrata može se geometrijski potvrditi zbroj površina.
Ishod:
Učenici razumiju Pitagorin poučak kroz vizualni i intuitivni način, razvijajući osjećaj za površinu i proporcionalnost.
2. Dokaz pomoću algebre
Ideja dokaza:
Ovaj dokaz koristi algebru za izračunavanje površine zajedničkog kvadrata koji se sastoji od pravokutnog trokuta. Trokut se smješta unutar kvadrata, a preostali dijelovi se koriste za dokaz.
Postupak:
1. Površina kvadrata se izražava na dva različita načina:
- Kao zbroj površina kvadrata na katetama.
- Kao površina kvadrata na hipotenuzi.
2. Uspoređivanjem tih izraza algebarski se dokazuje jednakost.
Ishod:
Učenici povezuju geometrijske koncepte s algebrom, razvijajući razumijevanje logičke strukture dokaza.
3. Dokaz pomoću sličnosti trokuta
Ideja dokaza:
Koristi se koncept sličnosti pravokutnih trokuta. Prave se dva manja trokuta unutar izvornog trokuta, koji su međusobno slični.
Postupak:
1. Postavlja se omjer stranica sličnih trokuta.
2. Kroz proporcionalnost stranica dokazuje se Pitagorin poučak.
Ishod:
Učenici bolje razumiju koncept sličnosti i povezanost proporcija u geometriji.
Zaključak
Ovi dokazi ne samo da potvrđuju valjanost Pitagorinog poučka, već omogućuju učenicima da razumiju osnovne ideje geometrije, algebre i proporcionalnosti. Svaki dokaz pruža jedinstveni pogled na teorem, a izbor ovisi o vrsti pristupa koji učenicima najviše odgovara.
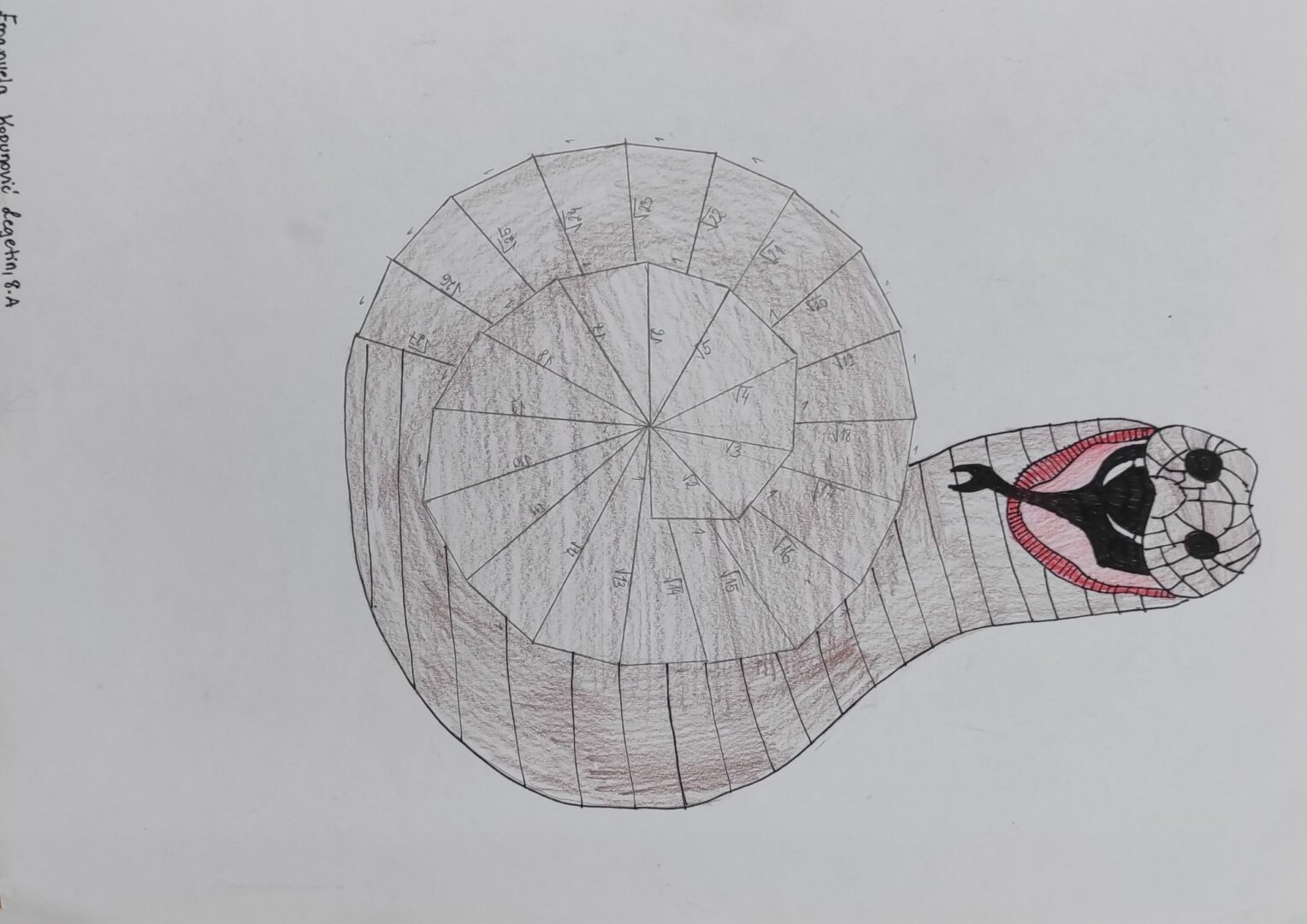
Spirala drugog korijena
Spirala drugog korijena – matematička ljepota i povezanost s prirodom
Spirala drugog korijena (poznata i kao *√2 spirala* ) fascinantan je geometrijski koncept koji omogućuje vizualizaciju kvadratnih korijena pomoću pravilnog rasporeda pravokutnih trokuta.
Zaključak
Spirala drugog korijena nije samo matematička konstrukcija – ona je *veza između apstraktne matematike i stvarnog svijeta* . Kroz ovaj projekt, učenici osmih razreda mogu naučiti kako se matematički obrasci ponavljaju u prirodi, umjetnosti i arhitekturi, razvijajući time dublje razumijevanje geometrije i proporcija.
Teselacija Pitagorin poučak
Teselacija pomoću pravokutnih trokuta je fascinantan matematički koncept koji se koristi u geometriji, dizajnu i umjetnosti.
Ishodi učenja
1.Razumijevanje geometrije i teselacija
– Učenici će naučiti kako se pravokutni trokuti mogu koristiti za prekrivanje ravnine bez praznina i preklapanja.
– Razvit će svijest o simetriji, ponavljajućim uzorcima i matematičkim strukturama u prostoru.
2. Primjena matematičkih transformacija
– Razvijat će se koncepti osne i centralne simetrije, rotacije i translacije kroz teselaciju.
– Učenici će istražiti kako se različiti položaji pravokutnih trokuta mogu koristiti za stvaranje složenih uzoraka.
3.Povezanost s umjetnošću i arhitekturom
– Učenici će vidjeti kako se teselacije koriste u arhitekturi, dizajnu podova, zidova i mozaika.
– Razumjet će kako se matematički koncepti mogu povezati s estetskim vrijednostima.
4. Logičko razmišljanje i kreativnost
– Učenici će osmisliti vlastite uzorke koristeći pravokutne trokute i analizirati kako se oni mogu koristiti u praktične svrhe.
Prikazivanje rezultata i zaključak
Prezentacija projekta:
- Na kraju projekta, učenici će predstaviti svoje mozaike u obliku izložbe u učionici, uz objašnjenje kako su koristili Pitagorin poučak u kreiranju svojih uzoraka.
- Učenici će izložiti sve potrebne proračune, objašnjavajući kako su primijenili Pitagorinu poučak u svakom dijelu mozaika.
Zaključak: Projekt pomaže učenicima da ne samo razumiju Pitagorinu poučak i njezinu primjenu, već i da razviju kreativnost kroz umjetnost i matematiku. Mozaici postaju način da se pokaže praktična primjena matematičkih zakona u stvarnom svijetu, čineći matematičke pojmove vizualno privlačnima i lako razumljivima.
Tako će učenici ne samo naučiti Pitagorin poučak, već i usvojiti kako matematiku primijeniti u kreativnim, realnim situacijama!