Autor: Ana Martinčević
Projektni zadatak: “Istraživanje površine nepravilnog mnogokuta”
Učenici 7.a razreda na satima matematike produbljuju svoje znanje kroz cjelinu Mnogokuti.
Nakon usvajanja površine mnogokuta imali su projekt.
Za potrebe projekta upoznali su matematičara Georg Alexander Picka i Pickovu formulu.
Cilj: Učenici će naučiti kako izračunati površinu nepravilnog mnogokuta koristeći metode dijeljenja na jednostavnije oblike.
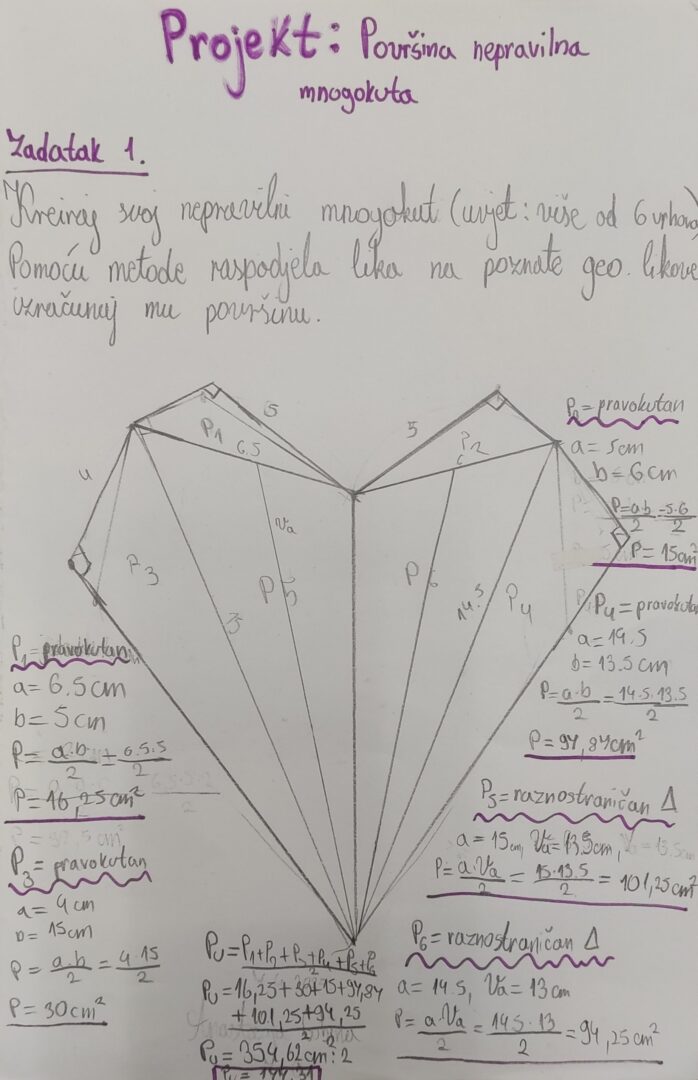
1.Zadatak:
Osmišljavanje vlastitog mnogokuta
- svaki učenik treba nacrtati nepravilni mnogokut na papiru ili u digitalnom alatu (može biti tlocrt neke zamišljene prostorije, vrta ili parcele).
- dimenzije stranica mnogokuta moraju biti jasno označene (dopušteno je koristiti ravnalo ili softver).
Dijeljenje mnogokuta na jednostavnije oblike:
- učenici trebaju podijeliti nepravilni mnogokut na manje, pravilne oblike (trokute, pravokutnike, trapeze).
- identificirati svaki dio unutar mnogokuta.
Izračunavanje površine:
- izračunati površinu svakog lika pomoću poznatih formula:
- zbrojiti sve pojedinačne površine da bi se dobila ukupna površina mnogokuta.
Prezentacija:
-učenici će prezentirati svoje mnogokute i prikazati korake izračuna površine putem plakata, PowerPoint prezentacije ili makete.
- objasniti metode koje su koristili za podjelu i izračun, te kako bi se njihovo rješenje moglo primijeniti u stvarnom životu (npr. mjerenje površine zemljišta).
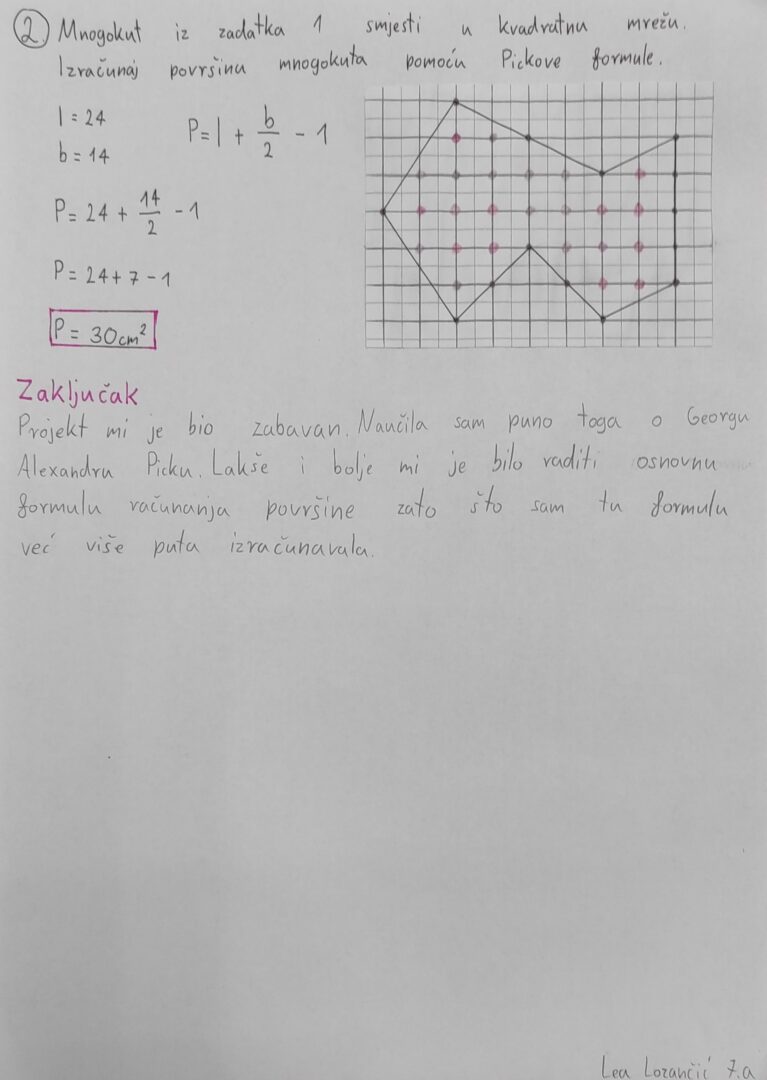
Zadatak 2. Primjena Pickove formule na površinu mnogokuta
Cilj: Učenici će naučiti koristiti Pickovu formulu za izračunavanje površine mnogokuta na koordinatnoj mreži.
Pronađi kako glasi Pickova formula. Istražiti povijesni kontekst Pickove formule: Tko je bio Georg Alexander Pick i kako je razvio ovu formulu?
Uvod u Pickovu formulu:
- učitelj objašnjava Pickovu formulu i daje jednostavan primjer na koordinatnoj mreži.
Crtanje mnogokuta:
- učenici dobivaju koordinatnu mrežu na papiru ili u digitalnom formatu.
- zadatak je nacrtati nepravilni mnogokut iz prvog dijela projekta na mreži, osiguravajući da su svi vrhovi mnogokuta na točkama mreže.
Brojanje točaka:
- učenici broje:
-unutarnje točke unutar mnogokuta
-rubne točke na granici mnogokuta
Izračunavanje površine:
- učenici koriste Pickovu formulu kako bi izračunali površinu svog mnogokuta.
5. Usporedba:
- učenici uspoređuju svoja rješenja s površinama izračunanim drugim metodama (npr. dijeljenje na trokute i pravokutnike) kako bi provjerili točnost Pickove formule.
Prezentacija:
- Svaki učenik predstavlja svoj mnogokut, proces izračuna i svoje zaključke o efikasnosti Pickove formule.